Distribución hipergeométrica

Función de probabilidad de la distribución hipergeométrica para .Red: ; azul: ; Verde: .${\ Displaystyle n = 20}$${\ Displaystyle M = 20, N = 60}$${\ Displaystyle M = 20, N = 30}$${\ Displaystyle M = 50, N = 60}$

La distribución hipergeométrica es una distribución de probabilidad en estocástica . Es univariado y es una de las distribuciones de probabilidad discretas . A diferencia de la distribución hipergeométrica general , también se denomina distribución hipergeométrica clásica .

Los elementos se toman aleatoriamente de una población dicotómica en una muestra sin reemplazo . La distribución hipergeométrica luego proporciona información sobre la probabilidad con la que se producirá un cierto número de elementos en la muestra que tienen la propiedad deseada. Por tanto, esta distribución es importante para los controles de calidad , por ejemplo . ${\ Displaystyle n}$

La distribución hipergeométrica se basa en el modelo de urna sin reemplazo (ver también combinación sin repetición ). En este contexto, se considera específicamente una urna con dos tipos de bolas. Las bolas se quitan sin reemplazarlas. La variable aleatoria es el número de bolas del primer tipo en esta muestra. ${\ Displaystyle n}$ ${\ Displaystyle X}$

La distribución hipergeométrica describe así la probabilidad de que para elementos dados ("población de la circunferencia "), que tienen la propiedad deseada, se logren exactamente aciertos al seleccionar los especímenes ("muestra de la circunferencia ") . H. la probabilidad de éxito en los experimentos. ${\ Displaystyle N}$${\ Displaystyle N}$${\ Displaystyle M}$${\ Displaystyle n}$${\ Displaystyle n}$${\ Displaystyle k}$${\ Displaystyle X = k}$${\ Displaystyle n}$

Ejemplo 1: Hay 30 bolas en una urna, 20 de las cuales son azules, por lo que 10 no son azules. ¿Cuál es la probabilidad p de sacar exactamente trece bolas azules de una muestra de veinte bolas (sin reemplazarlas)? Respuesta: p = 0.3096. Esto corresponde a la barra azul en k = 13 en el diagrama "Función de probabilidad de la distribución hipergeométrica para n = 20".

Ejemplo 2: Hay 45 bolas en una urna, 20 de las cuales son amarillas. ¿Cuál es la probabilidad p de sacar exactamente cuatro bolas amarillas de una muestra de diez bolas? Respuesta: p = 0,269. El ejemplo se calcula a continuación .

definición

La distribución hipergeométrica depende de tres parámetros:

• el número de elementos en una población .${\ Displaystyle N}$
• el número de elementos con una determinada propiedad en este conjunto básico (el número de posibles éxitos).${\ Displaystyle M \ leq N}$
• el número de elementos en una muestra.${\ Displaystyle n \ leq N}$

La distribución ahora proporciona información sobre la probabilidad de que los elementos con la propiedad que se va a verificar (éxitos o aciertos) estén en la muestra. El espacio resultado es por lo tanto . ${\ Displaystyle k}$ ${\ Displaystyle \ Omega}$${\ Displaystyle \ {\ max \ {0, n + MN \}, \ dotsc, \ min \ {n, M \} \}}$

Una variable aleatoria discreta está sujeta a la distribución hipergeométrica con los parámetros , y , si son las probabilidades${\ Displaystyle X}$${\ Displaystyle M}$${\ Displaystyle N}$${\ Displaystyle n}$

${\ displaystyle h (k | N; M; n): = P (X = k) = {\ frac {\ displaystyle {M \ elige k} {NM \ elige nk}} {\ displaystyle {N \ elige n} }}}$

para los dueños. El coeficiente binomial denota " más ". Entonces escribe o . ${\ Displaystyle k \ in \ Omega}$${\ Displaystyle {\ tbinom {N} {n}}}$${\ Displaystyle N}$${\ Displaystyle n}$${\ Displaystyle X \ sim Hyp_ {N, M, n}}$${\ Displaystyle X \ sim H (N, M, n)}$

La función de distribución indica entonces la probabilidad de que en la muestra se encuentren como máximo elementos con la propiedad que se va a probar. Esta probabilidad acumulada es la suma${\ Displaystyle H (k \ mid N; M; n)}$ ${\ Displaystyle k}$

${\ Displaystyle H (k | N; M; n): = P \ left (X \ leq k \ right) = \ sum _ {y = 0} ^ {k} h \ left (y \ mid N; M; n \ right) = \ sum _ {y = 0} ^ {k} {\ frac {\ displaystyle {M \ elige y} {\ displaystyle {NM} \ elige {ny}}} {\ displaystyle {N \ elige n }}}}$.

Parametrización alternativa

Ocasionalmente también se le llama función de probabilidad.

${\ Displaystyle Hyp_ {B_ {1}, B_ {2}, n} (\ {k \}): = {\ frac {\ displaystyle {B_ {2} \ elige k} {B_ {1} \ elige nk} } {\ Displaystyle {B_ {1} + B_ {2} \ Choose n}}}}$

usado. Esto va con y en la variante anterior. ${\ Displaystyle N = B_ {1} + B_ {2}}$${\ Displaystyle M = B_ {2}}$

Propiedades de la distribución hipergeométrica

Simetrías

Se aplican las siguientes simetrías:

• Intercambia bolas extraídas y aciertos: ${\ Displaystyle h (k | N; M; n) = h (k | N; n; M)}$
• Intercambia éxitos y fracasos: ${\ Displaystyle h (k | N; M; n) = h (nk | N; NM; n)}$

Valor esperado

El valor esperado de la variable aleatoria distribuida hipergeométricamente es ${\ Displaystyle X}$

${\ displaystyle \ operatorname {E} (X) = \ sum _ {k = 0} ^ {n} k {\ frac {\ displaystyle {M \ elige k} {\ displaystyle {NM} \ elige {nk}}} {\ Displaystyle {N \ elige n}}} = n {\ frac {M} {N}}}$.

modo

El modo de distribución hipergeométrica es

${\ Displaystyle \ left \ lfloor {\ frac {(n + 1) (M + 1)} {N + 2}} \ right \ rfloor}$.

Aquí está el corchete gaussiano . ${\ Displaystyle \ lfloor \ cdot \ rfloor}$

Diferencia

La varianza de la variable aleatoria distribuida hipergeométricamente es ${\ Displaystyle X}$

${\ displaystyle \ operatorname {Var} (X) = \ sum _ {k = 0} ^ {n} k ^ {2} {\ frac {\ displaystyle {M \ elige k} {\ displaystyle {NM} \ elige { nk}}} {\ displaystyle {N \ elige n}}} - \ left (n {\ frac {M} {N}} \ right) ^ {2} = n \, {\ frac {M} {N} } \ left (1 - {\ frac {M} {N}} \ right) {\ frac {Nn} {N-1}}}$,

La última fracción es el llamado factor de corrección (corrección de finitud ) en el modelo sin reemplazo.

Torcedura

La asimetría de la distribución hipergeométrica es

${\ Displaystyle \ operatorname {v} (X) = {\ frac {(N-2M) (N-1) ^ {\ frac {1} {2}} (N-2n)} {[nM (NM) ( Nn)] ^ {\ frac {1} {2}} (N-2)}}}$.

Función característica

La función característica tiene la siguiente forma:

${\ Displaystyle \ phi _ {X} (t) = {{{NM \ elige n} \, _ {2} F_ {1} (- n, -M; NM-n + 1; e ^ {it}) } \ over {N \ choose n}}}$

Por lo que denota la función hipergeométrica gaussiana . ${\ Displaystyle _ {2} F_ {1} (\ cdot; \ cdot; \ cdot)}$

Función generadora de momentos

La función generadora de momentos también se puede expresar usando la función hipergeométrica:

${\ Displaystyle M_ {X} (t) = {\ frac {{NM \ elige n} \, _ {2} F_ {1} (- n, -M; NM-n + 1; e ^ {t}) } {N \ elija n}}}$

Función generadora de probabilidad

La función generadora de probabilidad se da como

${\ Displaystyle m_ {X} (t) = {\ frac {{NM \ elige n} \, _ {2} F_ {1} (- n, -M; NM-n + 1; t)} {N \ elige n}}}$

Relación con otras distribuciones

Relación con la distribución binomial

A diferencia de la distribución binomial , con la distribución hipergeométrica, las muestras no se devuelven al depósito para su posterior selección. Si el tamaño de la muestra es relativamente pequeño (aproximadamente ) en comparación con el tamaño de la población , las probabilidades calculadas por la distribución binomial y la distribución hipergeométrica no difieren significativamente entre sí. En estos casos, la aproximación se suele realizar mediante la distribución binomial, que es matemáticamente más fácil de manejar. ${\ Displaystyle n}$${\ Displaystyle N}$${\ Displaystyle n / N <0 {,} 05}$

Relación con la distribución de Pólya

La distribución hipergeométrica es un caso especial de la distribución de Pólya (elegir ). ${\ Displaystyle c = -1}$

Relación con el modelo de urna

La distribución hipergeométrica surge de la distribución uniforme discreta a través del modelo de urna . De una urna con un total de bolas se colorean y se extraen bolas. La distribución hipergeométrica indica la probabilidad de que se dibujen esferas de colores. De lo contrario, la distribución binomial también se puede utilizar para modelar en la práctica. Vea también el ejemplo. ${\ Displaystyle N}$${\ Displaystyle M}$${\ Displaystyle n}$${\ Displaystyle \ max \ {0, n + MN \} \ leq k \ leq \ min \ {n, M \}}$${\ Displaystyle k}$

Relación con la distribución hipergeométrica multivariante

La distribución hipergeométrica multivariante es una generalización de la distribución hipergeométrica. Responde a la pregunta sobre el número de bolas de un color extraídas de una urna si la urna contiene más de dos colores distinguibles de bolas. Para dos colores concuerda con la distribución hipergeométrica.

Ejemplos de

Varios ejemplos

Hay 45 bolas en un recipiente, 20 de las cuales son amarillas. Se retiran 10 bolas sin reponer.

La distribución hipergeométrica indica la probabilidad de que exactamente x = 0, 1, 2, 3, ..., 10 de las bolas extraídas sean amarillas.

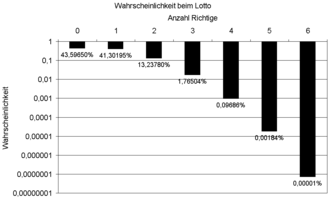
Un ejemplo de la aplicación práctica de la distribución hipergeométrica es la lotería : en la lotería de números hay 49 bolas numeradas; 6 de estos se dibujarán en el sorteo; Se cruzan 6 números en el billete de lotería.

${\ Displaystyle h (x | 49; 6; 6)}$indica la probabilidad de lograr exactamente x = 0, 1, 2, 3, ..., 6 "aciertos".

• Probabilidad en la lotería alemana
• 

  en aplicación lineal

• 

  en aplicación logarítmica

Ejemplo de cálculo detallado para las bolas

Para el ejemplo de las bolas de colores dadas anteriormente, se determinará la probabilidad de que resulten exactamente 4 bolas amarillas.

Número total de bolas	${\ Displaystyle N = 45}$
Número con la propiedad "amarillo"	${\ Displaystyle M = 20}$
Tamaño de la muestra	${\ Displaystyle n = 10}$
Apuntado al amarillo	${\ Displaystyle x = 4}$

Entonces . ${\ Displaystyle h (4 | 45,20,10)}$

La probabilidad resulta de:

Número de posibilidades para elegir exactamente 4 bolas amarillas (y por lo tanto exactamente 6 moradas)

dividido por

Número de formas de elegir exactamente 10 bolas de cualquier color

Hay

${\ Displaystyle {M \ Choose x} = {20 \ Choose 4} = 4 \, 845}$

Formas de elegir exactamente 4 bolas amarillas.

Hay

${\ displaystyle {{NM} \ choose {nx}} = {25 \ choose 6} = 177 \, 100}$

Formas de elegir exactamente 6 bolas moradas.

Dado que cada "posibilidad amarilla" se puede combinar con cada "posibilidad púrpura", esto da como resultado

${\ Displaystyle {M \ choose x} \ times {{NM} \ choose {nx}} = 4 \ .845 \ times 177 \, 100 = 858 \, 049 \, 500}$

Posibilidades para exactamente 4 bolas amarillas y 6 moradas.

Hay en total

${\ Displaystyle {N \ Choose n} = {45 \ Choose 10} = 3 \, 190 \, 187 \, 286}$

Formas de sacar 10 bolas.

Entonces obtenemos la probabilidad

${\ displaystyle P (X = 4) = h (4 | 45; 20; 10) = {\ frac {{20 \ elija 4} {25 \ elija 6}} {45 \ elija 10}} = {\ frac { 4 \, 845 \ cdot 177 \, 100} {3 \, 190 \, 187 \, 286}} \ approx 0 {,} 2690}$,

es decir, en alrededor del 27 por ciento de los casos, se eliminan exactamente 4 bolas amarillas (y 6 púrpuras).

Alternativamente, el resultado también se puede encontrar usando la siguiente ecuación

${\ displaystyle P (X = 4) = h (4 | 45; 10; 20) = {\ frac {{10 \ choose 4} {35 \ choose 16}} {45 \ choose 20}} \ approx 0 {, } 2690}$

Hay 4 bolas amarillas en la muestra . Las bolas amarillas restantes (16) están en las 35 bolas restantes que no forman parte de la muestra. ${\ Displaystyle n = 10}$

Valores numéricos para los ejemplos

enlaces web

• Calculadora de probabilidades simples y acumulativas de la distribución hipergeométrica

Evidencia individual

1. ↑ Hans-Otto Georgii: Estocástico . Introducción a la teoría de la probabilidad y la estadística. 4ª edición. Walter de Gruyter, Berlín 2009, ISBN 978-3-11-021526-7 , págs. 36 , doi : 10.1515 / 9783110215274 .