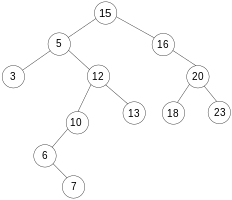
Árbol binario
Los árboles binarios son la subespecie de árboles más utilizada en informática . A diferencia de otros tipos de árboles, los nodos de un árbol binario solo pueden tener un máximo de dos descendientes directos.
Por lo general, se requiere que los nodos secundarios se puedan dividir claramente en secundarios izquierdo y derecho . Un ejemplo claro de un árbol binario de este tipo es el árbol genealógico , en el que, sin embargo, los nodos secundarios deben modelar a los padres.
Un árbol binario está vacío o consta de una raíz con un subárbol izquierdo y derecho, que a su vez son árboles binarios. Si un subárbol está vacío, el nodo secundario correspondiente se llama perdido.
La mayoría de las veces, la raíz se coloca en la parte superior y las hojas en la parte inferior en representaciones gráficas (como la de la derecha) . En consecuencia, un camino desde la raíz hacia la hoja es uno de arriba hacia abajo.
Condiciones
Los términos nodo y borde se toman de los gráficos. El borde está dirigido por definición (también: arco o flecha ). Si está lo suficientemente claro en el contexto, solo se denominará una ventaja.
En el caso de gráficos dirigidos , a un nodo se le puede asignar tanto un grado de salida como un grado de entrada . Los árboles binarios generalmente se ven como árboles externos . En tal árbol enraizado hay exactamente un nodo con el grado de entrada 0. Se llama raíz . Todos los demás nodos tienen el nivel de entrada 1. El nivel de salida es el número de nodos secundarios y está limitado a un máximo de dos en el árbol binario. Esto significa que su orden como árbol externo es ≤ 2 . Los nodos con grado ≥ 1 se denominan nodos internos , los de grado 0 se denominan hojas o nodos externos .
En la literatura, a menudo hay una visión en la que todos los nodos llevan información y no aparecen hojas externas. Luego, con árboles binarios, y solo allí, ocasionalmente existe la designación de media hoja para un nodo con grado 1 (a veces en inglés: nodo sin ramificación ).
La altura de un árbol enraizado es la profundidad máxima que se produce. Sin embargo, muchos autores lo establecen uno más alto, porque al árbol vacío se le puede dar la altura 0 y al árbol que consiste solo en la raíz se le puede asignar la altura 1, lo que permite acortar ciertas definiciones recursivas. (Y dado que la profundidad es un atributo de un nodo, pero la altura es un atributo de todo el árbol, no es necesario que haya confusión).
- tenga en cuenta
En este artículo se mantiene el último punto de vista :
- Todos los nodos, incluida la raíz y las hojas, transportan información ("almacenamiento orientado a nodos").
- La altura del árbol es el número máximo de niveles de nodos.
Un árbol binario se llama ordenado si cada nodo interno tiene un hijo izquierdo y posiblemente también derecho (y no solo un hijo derecho), y el nodo izquierdo es "más pequeño" y el nodo derecho es "más grande" que el nodo en consideración. Se llama completo si cada nodo es una hoja (es decir, no tiene un hijo) o tiene dos hijos (es decir, un hijo izquierdo y otro derecho), es decir, no hay media hoja . Los términos saturado o estricto también se utilizan ocasionalmente para la propiedad completa . Se dice que los árboles binarios completos están completos cuando todas las hojas tienen la misma profundidad , donde la profundidad de un nodo se define como el número de arcos hasta la raíz.
El árbol binario se llama degenerado si cada nodo es una hoja (el número de hijos es 0) o una media hoja (el número de hijos es 1). En este caso, el árbol representa una lista.Las formas especiales son las listas ordenadas, en las que un árbol consta solo de elementos secundarios de izquierda o derecha.
propiedades
- Así como un árbol con nudos tiene bordes , un árbol binario con nudos tiene bordes.
- Un árbol binario con nodos tiene puntos de inserción (inmediatos) .
- Un árbol binario con hojas y medias hojas tiene un punto de inserción en cada media hoja y dos puntos de inserción (inmediatos) en cada hoja .
- Si se calcula el número de nodos internos .
Combinatoria
El número de árboles binarios con nodos corresponde al número de posibilidades para encerrar completamente una secuencia de caracteres de símbolos ordenados, que están separados por matemáticos operadores para una combinación de dos dígitos , por ejemplo adición , substracción , multiplicación o división , en soportes . El orden de los números o elementos , por ejemplo matrices , es fijo. La operación no tiene que ser asociativa o conmutativa .
Cada nodo corresponde a un enlace de dos dígitos y para cada nodo el subárbol izquierdo corresponde a la expresión izquierda y el subárbol derecho corresponde a la expresión derecha del enlace.
Por ejemplo, hay que poner entre paréntesis una cadena , lo que se puede hacer de cinco formas distintas:
Un ejemplo explícito de resta es
No se permite agregar paréntesis redundantes alrededor de una frase entre paréntesis o la frase completa.
Hay un árbol binario con 0 nodos y todos los demás árboles binarios se caracterizan por la combinación de su subárbol izquierdo y derecho . Si estos tienen subárboles o nodos , todo el árbol tiene los nodos. Por lo tanto, el número de árboles binarios con nodos tiene la siguiente descripción recursiva y para cualquier entero positivo . De ello se deduce que el número catalán está con índice . Aplica
| Número de árboles binarios | |
|---|---|
| norte | C n |
| 1 | 1 |
| 2 | 2 |
| 3 | 5 |
| Cuarto | 14 |
| 5 | 42 |
| Sexto | 132 |
| Séptimo | 429 |
| Octavo | 1430 |
Aplicaciones
Árbol de búsqueda binaria
La aplicación más importante de los árboles binarios en la práctica son los árboles de búsqueda binaria , que incluyen los árboles AVL , los árboles rojo-negro y los árboles esparcidos . En los árboles de búsqueda hay "claves" en cada nodo, según las cuales los nodos se ordenan "linealmente" en el árbol. Una búsqueda lo más eficiente posible se basa entonces en este orden .
Árbol parcialmente ordenado
Un árbol parcialmente ordenado T es un árbol especial,
- cuyos nodos están marcados
- cuyas marcas provienen de un rango ordenado de valores
- en el que lo siguiente se aplica a cada subárbol U con la raíz x : Todos los nodos de U están marcados como mayores que x o iguales ax .
Intuitivamente, esto significa: La raíz de cada subárbol representa un mínimo para este subárbol Los valores del subárbol aumentan en la dirección de las hojas o permanecen iguales.
Estos árboles se utilizan a menudo en montones .
Árbol binario completo y árbol binario completamente equilibrado
Un árbol binario completo es un árbol binario completo (todos los nodos tienen 2 o 0 hijos) en el que todas las hojas tienen la misma profundidad. Inductivamente, se puede demostrar que un árbol binario completo de altura , que a menudo se denomina precisa
- Nodo,
- nodos internos (no hoja, pero posiblemente raíz),
- Nudos en profundidad para , así que en particular
- sale de
posee.
Un árbol binario completamente equilibrado es un árbol binario completo en el que las distancias desde la raíz hasta dos hojas cualesquiera difieren en no más de 1. Un árbol binario completo es un árbol binario completamente equilibrado. (Compare el árbol balanceado y el árbol AVL ).
Más árboles binarios
Una representación de un árbol binario en el que los nodos están representados por triángulos rectángulos y los arcos por rectángulos se llama árbol binario pitagórico .
Incluso los árboles de Fibonacci y los montones binarios se basan en árboles binarios.
Representación y acceso
La figura muestra un tipo de almacenamiento obvio. Corresponde aproximadamente a las estructuras C:
struct knoten { // 1 Objekt = 1 Knoten
char schlüssel;
struct knoten * links; // linkes Kind
struct knoten * rechts; // rechtes Kind
} object;
struct knoten * anker; // Zeiger auf die Wurzel
Para distinguir mejor entre los objetos, se les asignan las teclas "F", "G", "J" y "P". Estas claves también se utilizan como objetivos de referencia para simplificar (en lugar de direcciones de memoria reales ). Como de costumbre, un puntero con valor 0 debe expresar que no se hace referencia a ningún objeto, es decir, que no hay un niño en este punto.
La gran ventaja del árbol en comparación con la matriz es la gestión de la memoria más flexible: con la creación o desaparición de un objeto, la memoria que lo representa también puede surgir o desaparecer, mientras que las entradas individuales de la matriz se conectan permanentemente a él.
Índice en orden
Si en cada nodo se mantiene el número de elementos del subárbol asociado, la búsqueda de un elemento mediante su índice en orden se puede realizar de forma muy similar a la búsqueda con una clave en el árbol de búsqueda binaria . Sin embargo, esto tiene la implicación desventajosa de que las operaciones de inserción y eliminación siempre requieren correcciones hasta la raíz, que luego también cambia los índices en orden de los nodos. Por lo tanto, el procedimiento debería tener un valor cuestionable con árboles binarios no estáticos, y con árboles binarios estáticos, el índice de matriz ordinario es superior en términos de tiempo de ejecución.
El esfuerzo es donde está la altura del árbol.
Índice izquierdo / derecho
Cada nodo se puede especificar con precisión mediante una cadena de longitud variable de dígitos binarios. El requisito podría ser el siguiente:
- Un "0" al principio (al mismo tiempo al final) corresponde al árbol binario vacío.
- Un "1" al principio permite acceder a la raíz.
- Un "0" o "1" posterior permite el acceso al niño izquierdo o derecho.
Por tanto, se puede asignar claramente una cadena binaria a cada nodo de un árbol binario.
En el caso de árboles de altura equilibrada , la longitud de la cadena binaria está limitada por, de modo que puede caber en un entero sin signo . Una codificación concebible de la longitud variable en una palabra de longitud fija permite que la cadena binaria comience después del primer "1".
El esfuerzo máximo para un acceso es .
Representación por una matriz
Un árbol binario se puede representar mediante una matriz , cuya longitud corresponde esencialmente al número de nodos en el árbol, más precisamente: con que la altura del árbol. Se puede encontrar una disposición en la búsqueda binaria en la matriz .
Otro tipo de representación comienza con la indexación en 1 con referencia a la raíz. Luego continúa “línea por línea”: todos los nodos de la misma profundidad se numeran consecutivamente de izquierda a derecha. Eso significa: leer la matriz desde la izquierda corresponde a un recorrido de orden de nivel (o primer recorrido de ancho) del árbol. Si el árbol binario no está completamente ocupado, los nodos omitidos deben llenarse con marcadores de posición, de modo que se desperdicien las celdas de memoria.
Esta numeración tiene la agradable propiedad de que se pueden calcular fácilmente los índices de los nodos conectados. En la matriz A, sea A i un nodo, entonces A 2 i es su hijo izquierdo y A 2 i +1 su hijo derecho; la mitad redondeada se refiere al padre A j .
En genealogía , este esquema de indexación también se conoce como numeración de Kekule .
Dado que no se requieren punteros explícitos a los nodos secundarios o padres al mapear un árbol binario en una matriz, esta estructura de datos también se conoce como una estructura de datos implícita.
Una aplicación de esta representación es el montón binario , que se utiliza para ordenar elementos.
El recorrido
Atravesar se refiere al examen sistemático de los nodos del árbol en un orden determinado. De las diversas opciones para atravesar los nodos de árboles binarios, se hace una distinción principalmente entre las siguientes variantes:
Búsqueda en profundidad

secuencia completa de teclas 5 - 2 - 1 - 0 - 0 - 0 - 1 - 1 - 2 - 4 - 3 - 3 - 3 - 4 - 4 - 2 - 5 - 8 - 6 - 6 - 7 - 7 - 7 - 6 - 8 - 9 - 9 - X - X - X - 9 - 8 - 5 .
Pedido anticipado ( N LR, N en posición roja):
5-2-1-0-4-3-8-6-7-9-X ;
En orden (L N R, N en posición verde):
0-1-2-3-4-5-6-7-8-9-X ;
Pedido posterior (LR N , N en posición azul):
0–1–3–4–2–7–6 - X - 9–8–5 .
En el caso de la búsqueda en profundidad, primero se procesa una ruta completamente en profundidad ("profundidad primero") antes de que las ramas laterales se procesen en orden ascendente. La dirección de rotación alrededor del árbol es por defecto en sentido antihorario , es decir H. el subárbol izquierdo L se atraviesa antes que el derecho R ( recursivamente en cada caso ); la dirección de rotación inversa se denomina "inversa". Dependiendo de donde antes, entre o después de L, R se considere el nodo actual N , se hace una distinción entre los siguientes casos:
-
preorden u orden principal ( N - L - R ):
Primero se considera el nodo N y luego el L izquierdo y finalmente el subárbol derecho R se recorren recursivamente. -
post-orden u orden secundario ( LR - N ):
Primero se recorre recursivamente el subárbol izquierdo L , luego el subárbol derecho R y finalmente se considera el nodo N. -
en orden o orden simétrico ( L - N - R ):
Primero se recorre recursivamente el subárbol izquierdo L , luego se considera el nodo N y finalmente se recorre el subárbol derecho R de manera recursiva. Este orden corresponde al orden de las claves en los árboles de búsqueda binarios y es el que se da para la mayoría de las aplicaciones. -
orden inverso o orden antisimétrico ( R - N - L ):
Primero se atraviesa el subárbol derecho R , luego se considera el nodo N y finalmente se atraviesa el subárbol izquierdo L.
Implementaciones recursivas
La acción que se va a realizar en un nodo se realiza en la subrutina callbackque debe suministrar el usuario. Se puede realizar una determinada comunicación con el programa de llamada a través de la variable si es necesario param.
preOrder( N, callback, param) { // Startknoten N
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
if ( N.links ≠ null )
preOrder( N.links ); // rekursiver Aufruf
if ( N.rechts ≠ null )
preOrder( N.rechts ); // rekursiver Aufruf
}
postOrder( N, callback, param) {
if ( N.links ≠ null )
postOrder( N.links ); // rekursiver Aufruf
if ( N.rechts ≠ null )
postOrder( N.rechts ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
}
inOrder( N, callback, param) {
if ( N.links ≠ null )
inOrder( N.links ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
if ( N.rechts ≠ null )
inOrder( N.rechts ); // rekursiver Aufruf
}
revOrder( N, callback, param) {
if ( N.rechts ≠ null )
revOrder( N.rechts ); // rekursiver Aufruf
// Führe die gewünschten Aktionen am Knoten aus:
callback( N, param );
if ( N.links ≠ null )
revOrder( N.links ); // rekursiver Aufruf
}
Un recorrido por todo el árbol incluye exactamente una llamada de una de las funciones de recorrido recursivas por nodo. Por lo tanto, el esfuerzo (para el recorrido puro) en los nodos está en .
Implementación iterativa
Una implementación iterativa permite que se lleve a cabo un solo paso de cruce, una "iteración", desde un nodo al nodo vecino. De la forma habitual, puede configurar un bucle de programa para un intervalo con un inicio y un final, buscar los nodos en cuestión uno tras otro y programar las acciones deseadas para ellos.
Como ejemplo, aquí solo se muestra el recorrido en orden, lo cual es particularmente importante para los árboles de búsqueda binarios , ya que este orden corresponde al orden de clasificación.
inOrderNext( N, richtung ) { // Startknoten N
// richtung = 1 (Rechts = aufwärts = „in-order“)
// oder = 0 (Links = abwärts = „reverse in-order“)
Y = N.kind[richtung]; // 1 Schritt in die gegebene Richtung
if ( Y ≠ null ) {
gegenrichtung = 1 - richtung; // spiegele Links <-> Rechts
// Abstieg zu den Blättern über Kinder in der gespiegelten Richtung:
Z = Y.kind[gegenrichtung];
while ( Z ≠ null ) {
Y = Z;
Z = Y.kind[gegenrichtung];
}
return Y; // Ergebnisknoten: Blatt oder Halbblatt
}
// Aufstieg zur Wurzel über die Vorfahren der gegebenen Kindesrichtung:
Y = ;
do {
Z = Y;
Y = Z.elter;
if ( Y = null )
return null; // Knoten Z ist die Wurzel:
// d. h. es gibt kein Element mehr in dieser Richtung
} until ( Z ≠ Y.kind[richtung] );
// Y ist der erste Vorfahr in der gespiegelten Richtung
return Y; // Ergebnisknoten
}
Un recorrido por todo el árbol incluye un descenso (en la dirección del borde) y un ascenso (en la dirección opuesta) por borde . Un árbol con nodos tiene bordes, por lo que un recorrido general se realiza mediante pasos. El esfuerzo para un solo recorrido es, en promedio, y en el peor de los casos, con respecto a la altura del árbol.
Búsqueda en amplitud primero
primero en amplitud o en orden de nivel :
comenzando en la raíz del árbol, los niveles se recorren de izquierda a derecha.
Descenso al primer o último elemento
La búsqueda del primer o último elemento funciona de manera muy similar a una primera búsqueda en profundidad iterativa .
firstLast( binärBaum, richtung ) {
// richtung = Links (erstes) oder Rechts (letztes)
Y = binärBaum.wurzel;
if ( Y = null )
return null; // der Baum ist leer
// Abstieg zu den (Halb-)Blättern
do {
Z = Y;
Y = Z.kind[richtung];
} while ( Y ≠ null );
return Z; // Blatt oder Halbblatt
El esfuerzo es donde está la altura del árbol.
Insertar, punto de inserción
Se supone que ya se ha realizado la navegación a un punto de inserción. El punto de inserción significa un nodo y una dirección (derecha o izquierda). Un punto de inserción inmediato en un árbol binario es siempre una media hoja derecha (o izquierda), uno indirecto es el vecino inmediato en la dirección especificada y, junto con la dirección opuesta, especifica el mismo lugar en el árbol binario - de verdad inserción, sin embargo, la función de inserción tiene que subir hasta Descender la media hoja, que es el punto de inserción inmediato.
Para insertar, deje que el niño se refiera al nuevo elemento en la dirección requerida del nodo, para que se inserte correctamente. Por tanto, la complejidad de la operación de inserción es constante.
Una vez insertado, el nuevo elemento es una hoja del árbol binario.
En el siguiente ejemplo, un nodo con la clave J se inserta en un árbol binario en el punto de inserción (inmediato) ( M , izquierda); el indirecto sería ( G , derecha).
S S / \ / \ / \ / \ G W G W / \ / \ / \ ----> / \ D M D M / \ \ / \ / \ B F P B F J P
La inserción repetida en el mismo lugar puede llevar a que el árbol degenere en una lista lineal.
Claro
Al eliminar, debe distinguir significativamente más casos. Es importante, p. Ej. B. Cuántos hijos tiene el nudo.
Caso A: El nodo que se va a eliminar tiene como máximo un hijo.
Si el nodo es una hoja (nodo sin hijos), el nodo simplemente se elimina al eliminarlo. Si el nodo que se va a eliminar tiene exactamente un hijo, este se coloca en el lugar del nodo que se va a eliminar.
Caso B: el nodo que se va a eliminar tiene dos hijos.
En este caso, la eliminación se puede realizar utilizando tanto el subárbol izquierdo como el derecho. Sin embargo, para mantener la secuencia en orden, es inevitable un descenso a media hoja.
Una posibilidad es colocar el subárbol izquierdo en la posición donde estaba el nodo que se eliminará y agregar el subárbol derecho a la izquierda en su posición más a la derecha, como muestra el ejemplo ( se debe eliminar G ):
S S
/ \ / \
/ \ / \
G W D W
/ \ / \
/ \ ----> / \
D M B F
/ \ / \ \
B F J P M
\ / \
K J P
\
K
Sin embargo, los cambios en las alturas son menores si el nodo que se va a eliminar se reemplaza por un vecino (inmediato) en la secuencia en orden. En el ejemplo, F es el vecino izquierdo de G , por lo que está en el extremo derecho del subárbol izquierdo; J es el vecino derecho de G , por lo que está en el extremo izquierdo del subárbol derecho. El orden en el orden es F - G - J . El vecino izquierdo / derecho puede tener un subárbol izquierdo / derecho que debe adjuntarse al lugar donde estaba el vecino.
En el siguiente ejemplo, el nodo G que se va a eliminar se reemplaza por su vecino derecho J :
S S
/ \ / \
/ \ / \
G W J W
/ \ / \
/ \ / \
D M ----> D M
/ \ / \ / \ / \
B F J P B F K P
\
K
Para darle al árbol la menor oportunidad posible de volverse unilateral, puede alternar sistemáticamente entre el descenso hacia la izquierda y hacia la derecha. Si hay valores de equilibrio disponibles, tiene sentido preferir el descenso en el lado posiblemente más alto.
La eliminación repetida puede hacer que el árbol degenere en una lista lineal.
Debido a los inevitables descensos a las medias hojas, la complejidad de la operación de eliminación es en su peor momento , donde está la altura del árbol. Dado que el descenso corresponde a un solo recorrido y los descensos en un recorrido total son tan frecuentes como los ascensos, el valor medio de los niveles a descender converge exactamente a 1 para un número creciente de nodos.
Las figuras y el pseudocódigo muestran la eliminación de un elemento que tiene dos hijos y un nieto cercano de un árbol binario.
- Pseudocódigo
remove( binärBaum, knoten ) {
// Es sei angenommen, dass knoten.links ≠ null, knoten.rechts ≠ null
// und knoten.rechts.links ≠ null
knotenY = knoten.rechts;
while ( knotenY ≠ null ) {
knotenZ = knotenY;
knotenY = knotenZ.links;
}
// knotenZ ist der rechte Nachbar von knoten
if ( knotenZ.rechts ≠ null )
knotenZ.rechts.elter = knotenZ.elter;
knotenZ.elter.links = knotenZ.rechts;
knotenZ.rechts = knoten.rechts;
knoten.rechts.elter = knotenZ;
knotenZ.links = knoten.links;
knoten.links.elter = knotenZ; // knoten.links ≠ null
if ( knoten.elter.links = knoten )
knoten.elter.links = knotenZ;
else
knoten.elter.rechts = knotenZ;
knotenZ.elter = knoten.elter;
}
rotación
Con una rotación (вращение ( ruso para rotación ) en Adelson-Velsky y Landis) se puede transferir un árbol binario a otro y, por lo tanto, propiedades, en particular alturas de subárboles (por ejemplo, en árboles rojo-negro y árboles AVL ) o buscar profundidades de Influencia de los nodos (por ejemplo, en los árboles de distribución ). Dado que todos los nodos involucrados solo se mueven “verticalmente” durante una rotación, la secuencia en orden no cambia, por lo que el árbol permanece equivalente con respecto a esta secuencia (que es la secuencia de clasificación en los árboles de búsqueda).
Una rotación se puede especificar por la dirección de rotación hacia la izquierda o hacia la derecha y por la raíz del subárbol relevante. En lugar de los dos, también se puede especificar un nodo hijo, en esta aplicación que el pivote ( punto de pivote en adelante) de rotación. La dirección de rotación es opuesta a la dirección del niño. Por ejemplo, RotateLeft ( L ) hace que el nodo L se reduzca y su nodo secundario derecho se eleve (aquí como Pivot: R ). Sin embargo, no es una rotación continua, sino un balancín biestable, es decir , la inclinación de un borde (aquí: L ↘ R ) en su otra orientación ( L ↙ R ). Los requisitos
- Inversión de la orientación de un borde dirigido
- Conservación del orden en orden
- el cambio más pequeño posible en el árbol
dar como resultado ciertos ajustes en los nodos vecinos, a saber: (abajo) colgar al niño entre los dos nodos (aquí: m ) como el niño interno en el nodo inferior y (arriba) reemplazar al niño anterior con el padre (abuelo) (aquí : P ) a través del nudo superior.
P P
/ /
L RotateLeft(L) R
/ \ --------> / \
l \ <-------- / r
R RotateRight(R) L
/ \ / \
m r l m
- Declaración sobre RotateLeft ( L )
L se convierte de R hijo izquierdo . El original izquierda árbol niño m de R (el sub-árbol en el medio) es el árbol hijo derecho de L .
- Declaración RotateRight ( R )
R se convierte en L's hijo derecho . El derecho original árbol de niño m de L es el árbol hijo izquierdo R .
complejidad
En ambos casos, la suspensión del nuevo árbol también cambia desde arriba. Las suspensiones de los árboles niño exterior l y r se conservan.
Por lo tanto, se deben adaptar 3 enlaces, que se muestran en los gráficos. Como resultado, una rotación requiere un tiempo de ejecución constante .
Doble rotacion
Una doble rotación consta de dos rotaciones contrarrotantes (simples) que se llevan a cabo inmediatamente una tras otra. Un nodo se eleva en dos niveles. Es necesario , por ejemplo, al reequilibrar árboles AVL . El número de enlaces a ajustar es 5.
Las rotaciones triples también pueden ocurrir al dividir un árbol AVL.
Métrica de rotación
La distancia de rotación entre 2 árboles binarios con el mismo número de nodos es el número mínimo de rotaciones necesarias para transformar el primer árbol en el segundo. Con esta métrica, el conjunto de árboles binarios con nodos se convierte en un espacio métrico , porque la métrica cumple con la definición, la simetría y la desigualdad triangular . El espacio es un espacio métrico contiguo con un diámetro . Eso significa: Para 2 árboles binarios diferentes y hay un número natural y árboles binarios , de modo que con y para cada resultado de una rotación.
No está claro si existe un algoritmo polinomial para calcular la distancia de rotación.
Convierte una forma de un árbol binario en otra
Las siguientes conversiones no cambian el orden en orden. Además, sea el número de nodos del árbol.
- Un árbol binario se puede convertir en una lista ordenada con una inversión de espacio y tiempo.
- Dado que ingresar una sola entrada en una lista ordenada significa un esfuerzo constante, dada la complejidad de #traversing, el esfuerzo lineal es fácil de crear. Es más difícil realizar la entrada en el lugar , es decir, tomar el espacio para los punteros de la lista del espacio para el árbol binario.
- Una lista ordenada se puede convertir en un árbol binario completamente equilibrado con un gasto de tiempo .
- La forma de un árbol binario completamente equilibrado depende solo de su número de nodos. Si se va a construir un subárbol con una secuencia sin fisuras de nodos, entonces se asigna una secuencia sin fisuras de nodos al árbol hijo de la izquierda y uno de los nodos a la derecha . Esto significa que las distancias entre dos hojas cualesquiera desde la raíz se desvían entre sí en un máximo de 1, como debe ser.
- En un árbol binario, a cada nodo se le puede proporcionar el número de nodos en su subárbol con el gasto de tiempo .
- Al atravesar, el número de nodos por subárbol se puede formar y guardar en el nodo.
- Un árbol AVL se puede colorear como un árbol rojo-negro sin cambiar su forma .
- El conjunto de árboles AVL es un subconjunto real del conjunto de árboles rojo-negro. La evidencia allí también muestra que puede usar las alturas que anotó exactamente durante la carrera en orden para hacer el color rojo-negro.
Ver también
literatura
- Donald Knuth : El arte de la programación informática vol 1. Algoritmos fundamentales . 3. Edición. Addison-Wesley, 1997, ISBN 0-201-89683-4 , sección 2.3, p. 318 y siguientes.
- Horst Wettstein: Programación del sistema . 2ª Edición. Carl Hanser Verlag, 1980, ISBN 3-446-13217-1 .
- Lennart Krothaus: El árbol binario: un milagro de la informática . 3. Edición. MethiVerlag, 1998.
- Robert Sedgewick , Kevin Wayne: Algoritmos cuarta edición. (PDF) Pearson Education, 2011, ISBN 978-0-321-57351-3 .
enlaces web
- Ben Pfaff: Introducción a los árboles de búsqueda binaria y los árboles equilibrados . (PDF; 1675 kB) 2004 (inglés).
Evidencia individual
- ↑ En términos de cantidad, la altura llega al mismo valor que Knuth , quien además del nodo que lleva la llave (llamado "interno") también conoce los nodos "externos" , que pueden entenderse como puntos de inserción y que cambian la altura (según la primera definición) Incrementar 1.
- ↑ Los nombres se pueden encontrar, por ejemplo, en Knuth .
-
↑ S. a. Pfaff 2004 , p.58 "4.9.3.7 Avanzando al siguiente nodo" con una memoria de pila , llamada "Traverser", para el camino de regreso a la raíz. La solución presentada no la tiene; en cambio, requiere un puntero
elteral nodo principal. - ↑ Dado que no puede haber otro nodo entre los dos nodos, la secuencia en orden no cambia. Este enfoque fue propuesto por primera vez en 1962 por T. Hibbard (citado de #Sedgewick p. 410).
- ↑ GM Adelson-Velsky , EM Landis : Один алгоритм организации информации . En: Doklady Akademii Nauk SSSR . 146, 1962, págs. 263-266. (Ruso)
- ↑ La singularidad de estas adaptaciones se da (solo) para los árboles binarios . Porque si un borde L → R está inclinado, deben liberarse los nodos R anteriormente inferiores para el nuevo hijo, una "valencia" L. El único en la dirección correcta es la valencia de m . En L una valencia (que previamente señaló R ) se convierte en libre, que tiene la dirección de m y m tiene que tomar el relevo. La situación es muy similar en el extremo superior del borde.
- ↑ Daniel D. Sleator, Robert E. Tarjan, William P. Thurston: Distancia de rotación, triangulaciones y geometría hiperbólica. En: Revista de la Sociedad Matemática Estadounidense , 1, (3), 1988, págs. 647-681.