Error estándar

El error estándar o error de muestreo es una medida de dispersión para una función de estimación para un parámetro desconocido de la población . El error estándar se define como la desviación estándar del estimador, es decir, la raíz cuadrada positiva de la varianza . En las ciencias naturales y la metrología, también se utiliza el término incertidumbre estándar , acuñado por la GUM . ${\ Displaystyle {\ hat {\ vartheta}}}$${\ Displaystyle \ vartheta}$ ${\ Displaystyle \ sigma ({\ hat {\ vartheta}}) = + {\ sqrt {\ operatorname {Var} ({\ hat {\ vartheta}})}}}$${\ Displaystyle {\ hat {\ vartheta}}}$

En el caso de un estimador insesgado , el error estándar es, por lo tanto, una medida de la desviación promedio del valor del parámetro estimado del valor del parámetro verdadero. Cuanto menor sea el error estándar, más precisamente se puede estimar el parámetro desconocido utilizando el estimador. El error estándar depende, entre otras cosas, de

• el tamaño de la muestra y
• la varianza en la población.

En general, cuanto mayor es el tamaño de la muestra, menor es el error estándar; cuanto menor es la varianza, menor es el error estándar.

El error estándar también juega un papel importante en el cálculo de errores de estimación , intervalos de confianza y estadísticas de prueba .

interpretación

El error estándar proporciona una declaración sobre la calidad del parámetro estimado. Cuantos más valores individuales haya, menor será el error estándar y con mayor precisión se podrá estimar el parámetro desconocido. El error estándar hace que la dispersión medida (desviación estándar) de dos conjuntos de datos con diferentes tamaños de muestra sea comparable al normalizar la desviación estándar al tamaño de la muestra.

Si el parámetro desconocido se estima con la ayuda de varias muestras, los resultados variarán de una muestra a otra. Por supuesto, esta variación no proviene de una variación del parámetro desconocido (porque es fijo), sino de influencias aleatorias, p. Ej. B. Inexactitudes de medición. El error estándar es la desviación estándar de los parámetros estimados en muchas muestras. En general, reducir a la mitad el error estándar requiere cuadriplicar el tamaño de la muestra.

En contraste con esto, la desviación estándar representa la dispersión real en una población , que también está presente con la mayor precisión de medición y un número infinito de mediciones individuales (por ejemplo, para distribución de peso, distribución de tamaño, ingreso mensual). Muestra si los valores individuales están cerca unos de otros o si los datos están muy extendidos.

ejemplo

Suponga que estudia la población de niños de secundaria en términos de su desempeño en inteligencia. Entonces, el parámetro desconocido es el desempeño intelectual promedio de los niños que asisten a la escuela secundaria. Si se extrae una muestra aleatoria del tamaño (es decir, con niños) de esta población , el valor medio se puede calcular a partir de todos los resultados de la medición . Si, después de esta muestra, se extrae otra muestra aleatoria con el mismo número de hijos y se determina su valor medio, los dos valores medios no coincidirán exactamente. Si toma una gran cantidad de otras muestras aleatorias del alcance , entonces se puede determinar la dispersión de todos los valores medios determinados empíricamente alrededor del valor medio de la población. Esta extensión es el error estándar. Dado que la media de las medias muestrales es la mejor estimación de la media poblacional, el error estándar es la dispersión de las medias empíricas alrededor de la media poblacional. No muestra la distribución de inteligencia de los niños, sino la precisión de la media calculada. ${\ Displaystyle n}$${\ Displaystyle n}$${\ Displaystyle n}$${\ Displaystyle n}$${\ Displaystyle n}$

notación

Se utilizan varios términos para el error estándar para distinguirlo de la desviación estándar de la población y para dejar claro que es la dispersión del parámetro estimado de las muestras: ${\ Displaystyle \ sigma}$

• ${\ Displaystyle \ sigma _ {n}}$,
• ${\ Displaystyle \ sigma ({\ hat {\ vartheta}})}$ o
• ${\ Displaystyle \ sigma _ {\ hat {\ vartheta}}}$.

estimar

Dado que la desviación estándar de la población se incluye en el error estándar, la desviación estándar de la población debe estimarse utilizando un estimador que sea lo más preciso posible para estimar el error estándar. ${\ Displaystyle \ sigma}$

Intervalos y pruebas de confianza

El error estándar también juega un papel importante en los intervalos de confianza y las pruebas . Si el estimador es justo para las expectativas y al menos aproximadamente distribuido normalmente ( ), entonces es ${\ Displaystyle {\ hat {\ vartheta}}}$ ${\ Displaystyle {\ mathcal {N}} (\ vartheta, \ sigma ^ {2} ({\ hat {\ vartheta}}))}$

${\ displaystyle {\ frac {{\ hat {\ vartheta}} - \ vartheta} {\ sigma ({\ hat {\ vartheta}})}} \ approx {\ mathcal {N}} (0; 1)}$.

Sobre esta base, - Se pueden especificar intervalos de confianza para el parámetro desconocido : ${\ Displaystyle (1- \ alpha)}$${\ Displaystyle \ vartheta}$

${\ Displaystyle P ({\ hat {\ vartheta}} - z_ {1- \ alpha / 2} \ sigma ({\ hat {\ vartheta}}) \ leq \ vartheta \ leq {\ hat {\ vartheta}} + z_ {1- \ alpha / 2} \ sigma ({\ hat {\ vartheta}})) = 1- \ alpha}$

o formular pruebas, p. ej. B. si el parámetro asume un cierto valor : ${\ Displaystyle \ vartheta _ {0}}$

${\ Displaystyle H_ {0}: \ vartheta = \ vartheta _ {0}}$ vs. ${\ Displaystyle H_ {1}: \ vartheta \ neq \ vartheta _ {0}}$

y la estadística de prueba da como resultado:

${\ Displaystyle V = {\ frac {{\ hat {\ vartheta}} - \ vartheta _ {0}} {\ sigma ({\ hat {\ vartheta}})}} \ approx {\ mathcal {N}} ( 0; 1)}$.

${\ Displaystyle z_ {1- \ alpha / 2}}$es la - cuantil de la distribución normal estándar y es también el valor crítico para el ensayo formulado. Como regla general, debe estimarse a partir de la muestra, de modo que ${\ Displaystyle (1- \ alpha / 2)}$${\ Displaystyle \ sigma ({\ hat {\ vartheta}})}$

${\ displaystyle V = {\ frac {{\ hat {\ vartheta}} - \ vartheta _ {0}} {{\ hat {\ sigma}} ({\ hat {\ vartheta}})}} \ approx t_ { n-1}}$

se mantiene, donde es el número de observaciones. Porque , la distribución t puede aproximarse mediante la distribución normal estándar. ${\ Displaystyle n}$${\ Displaystyle n \ geq 30}$

Error estándar de la media aritmética

El error estándar de la media aritmética es el mismo

${\ Displaystyle \ sigma ({\ overline {X}}) = {\ frac {\ sigma} {\ sqrt {n}}}}$,

donde denota la desviación estándar de una sola medición. ${\ Displaystyle \ sigma}$

Derivación

La media de un tamaño de muestra se define por ${\ Displaystyle n}$

${\ Displaystyle {\ overline {x}} = {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} x_ {i}.}$

Mirando el estimador

${\ Displaystyle {\ overline {X}} = {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} X_ {i}}$

con variables aleatorias independientes distribuidas de forma idéntica con varianza finita , el error estándar se define como la raíz cuadrada de la varianza de . Usando las reglas de cálculo para las variaciones y la ecuación de Bienaymé, se calcula : ${\ Displaystyle X_ {1}, \ ldots, X_ {n}}$${\ Displaystyle \ sigma ^ {2}}$${\ Displaystyle {\ overline {X}}}$

${\ Displaystyle \ sigma ({\ overline {X}}) ^ {2} = \ operatorname {Var} \ left ({\ overline {X}} \ right) = \ operatorname {Var} \ left ({\ frac { 1} {n}} \ sum _ {i = 1} ^ {n} X_ {i} \ right) = {\ frac {1} {n ^ {2}}} \ operatorname {Var} \ left (\ sum _ {i = 1} ^ {n} X_ {i} \ right) = {\ frac {1} {n ^ {2}}} \ sum _ {i = 1} ^ {n} \ operatorname {Var} \ izquierda (X_ {i} \ right) = {\ frac {1} {n ^ {2}}} n \ sigma ^ {2} = {\ frac {\ sigma ^ {2}} {n}}}$

de donde se sigue la fórmula del error estándar. Si es cierto, se sigue análogamente ${\ Displaystyle \ operatorname {Var} (X_ {i}) = \ sigma _ {i} ^ {2}}$

${\ Displaystyle \ sigma ({\ overline {X}}) ^ {2} = {\ frac {1} {n ^ {2}}} \ sum _ {i = 1} ^ {n} \ sigma _ {i } ^ {2}}$.

Calculo de ${\ Displaystyle \ sigma}$

Suponiendo una distribución de la muestra, el error estándar se puede calcular utilizando la varianza de la distribución de la muestra:

• en la distribución binomial con parámetros${\ Displaystyle N, \, p}$

${\ Displaystyle \ sigma _ {{\ bar {x}}, \ mathrm {binom}} = {\ frac {\ sqrt {N \ cdot p \ cdot (1-p)}} {\ sqrt {n}}} }$,

• para la distribución exponencial con parámetros (valor esperado = desviación estándar = ):${\ Displaystyle \ lambda}$${\ Displaystyle 1 / \ lambda}$

${\ Displaystyle \ sigma _ {{\ bar {x}}, \ mathrm {exp}} = {\ frac {1} {\ lambda {\ sqrt {n}}}}}$

• y para la distribución de Poisson con parámetros (valor esperado = varianza = ):${\ Displaystyle \ lambda}$${\ Displaystyle \ lambda}$

${\ Displaystyle \ sigma _ {{\ bar {x}}, \ mathrm {poisson}} = {\ sqrt {\ frac {\ lambda} {n}}}}$

Designarlo

• ${\ Displaystyle \ sigma _ {{\ bar {x}}, \ mathrm {binom}}, \ sigma _ {{\ bar {x}}, \ mathrm {exp}}, \ sigma _ {{\ bar {x }}, \ mathrm {poisson}}}$ los errores estándar de las respectivas distribuciones, y
• ${\ Displaystyle n}$ el tamaño de la muestra.

Si se va a estimar el error estándar de la media, entonces la varianza se estima con la varianza de la muestra corregida . ${\ Displaystyle \ sigma ^ {2}}$

ejemplo

Para los datos de helado, se calcularon la media aritmética, su error estándar y la desviación estándar para los años 1951, 1952 y 1953 para el consumo per cápita de helado (medido en pintas ).

año	Promedio	Error estándar de la media	Desviación estándar	Numero de observaciones
1951	0.34680	0.01891	0.05980	10
1952	0.34954	0.01636	0.05899	13
1953	0.39586	0.03064	0.08106	Séptimo

Para los años 1951 y 1952, los valores medios estimados y las desviaciones estándar, así como los números de observación, son aproximadamente los mismos. Por lo tanto, los errores estándar estimados también dan aproximadamente el mismo valor. En 1953, por un lado, el número de observaciones es menor y la desviación estándar es mayor. Por lo tanto, el error estándar es casi el doble de los errores estándar de 1951 y 1952.

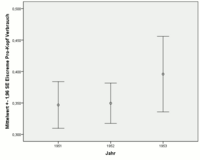
La representación gráfica puede realizarse mediante un diagrama de barras de error . Los intervalos de estimación del 95% para los años 1951, 1952 y 1953 se muestran a la derecha. Si la función muestral tiene una distribución al menos aproximadamente normal, los intervalos de estimación del 95% vienen dados por con y las medias muestrales y las varianzas muestrales. ${\ Displaystyle {\ bar {X}}}$${\ displaystyle {\ bar {x_ {j}}} \ pm 1 {,} 96 \ cdot s_ {j} / {\ sqrt {n_ {j}}}}$${\ displaystyle j = 1951.1952.1953}$${\ Displaystyle {\ bar {x}} _ {j}}$${\ Displaystyle s_ {j} ^ {2}}$

Aquí también se puede ver claramente que el valor medio para 1953 puede estimarse de manera más imprecisa que los valores medios para 1951 y 1952 (barra más larga para 1953).

Error estándar de los coeficientes de regresión en el modelo de regresión simple

El modelo de regresión clásico para regresión lineal simple supone que ${\ Displaystyle Y_ {i} = \ beta _ {0} + \ beta _ {1} x_ {i} + \ varepsilon _ {i}}$

• los términos de perturbación se distribuyen normalmente ,${\ Displaystyle \ varepsilon _ {i} \ sim \, (0, \ sigma ^ {2})}$
• los términos son independientes y
• los valores son fijos (es decir, sin variables aleatorias),${\ Displaystyle x_ {i}}$

con las observaciones realizadas al ejecutar. Para los estimadores${\ Displaystyle i = 1, \ ldots, n}$

${\ Displaystyle {\ hat {\ beta}} _ {1} = {\ frac {\ sum _ {i} (x_ {i} - {\ overline {x}}) (Y_ {i} - {\ overline { Y}})} {\ sum _ {i} (x_ {i} - {\ overline {x}}) ^ {2}}}}$ y

${\ displaystyle {\ hat {\ beta}} _ {0} = {\ overline {Y}} - {\ hat {\ beta}} _ {1} {\ overline {x}}}$

entonces resultados

${\ Displaystyle {\ hat {\ beta}} _ {1} \ sim {\ mathcal {N}} (\ beta _ {1}, \ sigma _ {{\ hat {\ beta}} _ {1}} ^ {2} \ cdot a_ {1}) \,}$y .${\ displaystyle {\ hat {\ beta}} _ {0} \ sim {\ mathcal {N}} (\ beta _ {0}, \ sigma _ {{\ hat {\ beta}} _ {0}} ^ {2} \ cdot a_ {0})}$

Los errores estándar de los coeficientes de regresión están dados por

${\ Displaystyle \ sigma _ {{\ hat {\ beta}} _ {1}} = \ operatorname {SD} ({\ hat {\ beta}} _ {1}) = \ sigma {\ sqrt {\ underbrace { \ frac {1} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} _ {=: a_ {1}}} } = \ sigma \ cdot {\ sqrt {a_ {1}}}}$

y

${\ Displaystyle \ sigma _ {{\ hat {\ beta}} _ {0}} = \ operatorname {SD} ({\ hat {\ beta}} _ {0}) = \ sigma {\ sqrt {\ underbrace { \ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i} ^ {2}} {n \ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} _ {=: a_ {0}}}} = \ sigma \ cdot {\ sqrt {a_ {0}}}}$.

Ejemplo : Para los datos del helado, se realizó una regresión lineal simple para el consumo per cápita de helado (medido en medio litro) con la temperatura media semanal (en Fahrenheit) como variable independiente. La estimación del modelo de regresión resultó en:

${\ displaystyle {\ text {Consumo per cápita}} = 0 {,} 20686 + 0 {,} 00311 \ cdot {\ text {Temperatura}}}$.

modelo	Coeficientes no estandarizados		Coeficientes estandarizados	T	Sig.
	Coeficientes de regresión	Error estándar
constante	0,20686	0.02470		8.375	0.000
temperatura	0,00311	0,00048	0,776	6.502	0.000

Aunque el coeficiente de regresión estimado para la temperatura media semanal es muy pequeño, el error estándar estimado arrojó un valor aún menor. La precisión con la que se estima el coeficiente de regresión es 6,5 veces más pequeña que el coeficiente en sí.

Relación con la probabilidad logarítmica

El término también se conoce como el error estándar del estimador de máxima verosimilitud , donde la función logarítmica de verosimilitud y representa la información de Fisher observada (la información de Fisher en lugar del estimador de ML ).${\ Displaystyle \ sigma ({\ hat {\ theta}} _ {ML}) = {\ frac {1} {\ sqrt {- {\ frac {\ parcial ^ {2}} {\ parcial \ theta ^ {2 }}} \ ell ({\ hat {\ theta}} _ {ML})}}}}$${\ Displaystyle \ ell (\ cdot) = \ log {\ mathcal {L}} (\ cdot)}$${\ estilo de visualización - {\ frac {\ parcial ^ {2}} {\ parcial \ theta ^ {2}}} \ ell ({\ hat {\ theta}} _ {ML})}$${\ Displaystyle {\ hat {\ theta}} _ {ML}}$

Ver también

• Error estándar de regresión

Evidencia individual

1. ↑ ^{a b} Koteswara Rao Kadiyala (1970): Prueba de la independencia de las perturbaciones de regresión. En: Econometrica , 38, 97-117.
2. ↑ ^{a b} dátiles helados. En: Data and Story Library , consultado el 16 de febrero de 2010
3. ↑ Suplemento: Intervalos de confianza y verosimilitud logarítmica. Consultado el 14 de julio de 2021 .