Zurra

Currying (especialmente en lingüística también Schönfinkeln ) es la conversión de una función con varios argumentos en una secuencia de funciones con un argumento cada una. Aunque el proceso fue inventado por Moses Schönfinkel en 1924 y pensado por Gottlob Frege alrededor de 1900, a menudo recibe su nombre de Haskell Brooks Curry , quien desarrolló ampliamente el proceso en teoría en 1958.

Procedimiento

Dada una función que toma n  argumentos. Si esto se aplica a un  argumento, solo lo consume y entrega otra función como un valor de función que aún requiere argumentos. Luego, la función devuelta se aplica a todos los argumentos adicionales. ${\ Displaystyle n-1}$

Expresado en tipos, se trata de convertir una función en una función modificada .${\ Displaystyle f \ colon A_ {1} \ times \ ldots \ times A_ {n} \ to B}$${\ Displaystyle f _ {\ mathrm {curry}} \ colon A_ {1} \ to (A_ {2} \ to (\ ldots (A_ {n} \ to B) \ ldots))}$

Una notación alternativa es , que se entiende como un operador que modifica las asignaciones de dígitos (para ) a un mapa de un solo dígito, cuyos valores de imagen son asignaciones de un solo dígito, etc., siendo todos los argumentos de la asignación original ejecutar en secuencia; formalmente: ${\ Displaystyle \ operatorname {curry} (f) = f _ {\ mathrm {curry}}}$${\ Displaystyle \ operatorname {curry}}$${\ Displaystyle n}$${\ Displaystyle n> 1}$

${\ Displaystyle \ operatorname {curry} \ colon (A_ {1} \ times \ ldots \ times A_ {n} \ to B) \, \ to \, (A_ {1} \ to (A_ {2} \ to ( \ ldots (A_ {n} \ to B) \ ldots)))}$.

El concepto de curry está relacionado pero (para ) diferente al de aplicación parcial como: ${\ Displaystyle n> 2}$

${\ Displaystyle f (a_ {1}, a_ {2}, \ ldots a_ {n-1}, \ cdot) \ colon A_ {n} \ to B, a_ {n} \ mapsto f (a_ {1}, a_ {2}, \ ldots a_ {n})}$,

${\ Displaystyle f (a_ {1}, \ underbrace {\ cdot, \ ldots, \ cdot} _ {(n-1) {\ text {-mal}}})) \ colon A_ {2} \ times \ ldots \ times A_ {n} \ to B, (a_ {2}, \ dots, a_ {n}) \ mapsto f (a_ {1}, a_ {2}, \ ldots a_ {n})}$.

En el caso de un solo dígito ( ), el curry no tiene ningún efecto: ${\ Displaystyle n = 1}$

${\ Displaystyle f _ {\ mathrm {curry}} = f}$,

en el caso de dos dígitos ( ) hay una conexión ${\ Displaystyle n = 2}$

${\ Displaystyle f _ {\ mathrm {curry}} \ colon A_ {1} \ to (A_ {2} \ to B), a_ {1} \ mapsto f (a_ {1}, \ cdot)}$, d. H. para todos :${\ Displaystyle a_ {1} \ in A_ {1}}$

${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) = f (a_ {1}, \ cdot)}$,

en el caso de tres dígitos ( ) se aplica a :${\ Displaystyle n = 3}$${\ Displaystyle a_ {1} \ in A_ {1}}$

${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) \ colon A_ {2} \ to (A_ {3} \ to B), a_ {2} \ mapsto f (a_ {1}, a_ {2}, \ cdot)}$, y adicionalmente :${\ Displaystyle a_ {2} \ in A_ {2}}$

${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) (a_ {2}) \ colon A_ {3} \ to B, a_ {3} \ mapsto f (a_ {1}, a_ {2 }, \ cdot)}$, d. H. ,${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) (a_ {2}) = f (a_ {1}, a_ {2}, \ cdot)}$

generalmente:

${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) (a_ {2}) \ dots (a_ {n}) = f (a_ {1}, a_ {2}, \ dots, a_ { n})}$,

${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) (a_ {2}) \ dots (a_ {n-1}) = f (a_ {1}, a_ {2}, \ dots, a_ {n-1}, \ cdot)}$.

En general, a menudo sucede que un mapeo de varios dígitos no se define para todas las combinaciones de valores de los conjuntos de portadores , es decir, solo para un subconjunto del producto cartesiano , es decir H. en (la gráfica de una) relación . Se puede hacer frente a esta situación ya sea permitiendo mapeos parciales en principio y adoptando formalmente las definiciones anteriores, o apegándose al concepto de mapas totales; en este último caso, los dominios de definición de las cifras involucradas dependen de la elección de parámetros que ya han sido definidos, como muestra el ejemplo de cifras de dos dígitos: ${\ Displaystyle A_ {1}, \ dots, A_ {n}}$${\ Displaystyle R = D_ {f} \ subseteq A_ {1} \ times \ cdots \ times A_ {n}}$

${\ Displaystyle f _ {\ mathrm {curry}} (a_ {1}) = f (a_ {1}, \ cdot)}$;

el rango de definición de esta figura depende de: ${\ Displaystyle a_ {1}}$

${\ Displaystyle \ {a_ {2} \ en A_ {2} | \ existe a_ {1} \ en A_ {1} \ dos puntos (a_ {1}, a_ {2}) \ en D_ {f} \} = R ^ {\ leftarrow} (\ {a \})}$,

de ahí la fibra arquetípica del dominio de definición entendido como relación .${\ Displaystyle a_ {1}}$${\ Displaystyle R = D_ {f}}$

Como es cierto para n = 1 , se puede usar para el mismo símbolo . A esto se le llama sobrecarga (ver también la firma (teoría de modelos) §Notas ).${\ Displaystyle f _ {\ mathrm {curry}} = f}$${\ displaystyle f _ {\ mathrm {curry}}}$${\ Displaystyle f}$

Ejemplos de

Notación lambda

Un ejemplo en notación lambda pretende aclarar el procedimiento, por lo que la función se define específicamente de la siguiente manera:

${\ Displaystyle \ lambda x \ y \ z \. \ x \ y \ z}$

Entonces, la función requiere 3 argumentos y los devuelve. La definición es equivalente a:

${\ Displaystyle \ lambda x. \ lambda y. \ lambda z \. \ x \ y \ z}$

Cuando la función se aplica a los argumentos a, byc, sucede lo siguiente:

${\ Displaystyle \ left (\ lambda x. \ lambda y. \ lambda z \. \ x \ y \ z \ right) \ a \ b \ c \ {\ mathsf {- \ The \ Application}}}$

${\ Displaystyle \ left (\ lambda y. \ lambda z \. \ a \ y \ z \ right) \ b \ c}$

${\ Displaystyle \ left (\ lambda z \. \ a \ b \ z \ right) \ c}$

${\ Displaystyle a \ b \ c \ {\ mathsf {- \ Result}}}$

Después de la función se ha aplicado a una , b y  c por primera vez , x en el cuerpo de la función se sustituye por el primer argumento  una . El resultado es una función que aún requiere los argumentos y y z . Esto se aplica inmediatamente a b y  c .

Sobrecarga

Suponga que tenemos una función de multiplicación de dos dígitos que multiplica dos enteros; H. asigna su producto a un par de números enteros: ${\ Displaystyle \ operatorname {mult}}$

${\ Displaystyle \ operatorname {mult} \ colon \, {\ begin {cases} \ mathbb {N} \ times \ mathbb {N} \ to \ mathbb {N} \\ (m, n) \ mapsto m * n \ finalizar {casos}}}$ Con ${\ Displaystyle \ operatorname {mult} (m, n) = m * n}$ 

Por definición, esta función se aplica a dos números naturales y se devuelve un número natural, por ejemplo . ${\ Displaystyle \ operatorname {mult} (2,3) = 6}$

Si el primer argumento ahora se completa (por ejemplo, con ) y el segundo se deja en blanco, se crea una ' función superior ' de un solo dígito , que a su vez acepta un argumento (adicional) y devuelve el producto con este parámetro fijo (el número ): ${\ Displaystyle 2}$${\ Displaystyle 2}$

${\ Displaystyle \ operatorname {mult} (2, \ cdot) \ colon \,}$ ${\ Displaystyle {\ begin {cases} \ mathbb {N} \ to \ mathbb {N} \\ n \ mapsto 2 * n \ end {cases}}}$,

y para cualquier primer argumento fijo : ${\ Displaystyle m \ in \ mathbb {N}}$

${\ Displaystyle \ operatorname {mult} (m, \ cdot) \ colon \,}$ ${\ Displaystyle {\ begin {cases} \ mathbb {N} \ to \ mathbb {N} \\ n \ mapsto m * n \ end {cases}} \,}$ .

Con una función de n dígitos, curar ahora significa llevar a cabo este proceso hasta que solo quede una función superior de un dígito. Para n = 2 tenemos:

${\ Displaystyle \ operatorname {mult} _ {\ mathrm {curry}} \ colon \, {\ begin {cases} \ mathbb {N} \ to (\ mathbb {N} \ to \ mathbb {N}) \\ m \ mapsto \ operatorname {mult} (m, \ cdot) \ end {cases}} \,}$ 

Dado que la designación como función de un dígito aún está vacante, puede estar sobrecargada, i. . H, en el caso individual, como entiende: ${\ Displaystyle \ operatorname {mult}}$${\ Displaystyle \ operatorname {mult}}$${\ Displaystyle \ operatorname {mult} _ {\ mathrm {curry}}}$

${\ Displaystyle \ operatorname {mult} (m) (n) = \ operatorname {mult} _ {\ mathrm {curry}} (m) (n) = \ operatorname {mult} (m, n) = m * n}$.

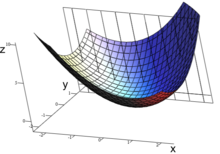
Ejemplo geométrico

f (x, y) = x ^ 2 + xy + y ^ 2

La situación para una función con dos argumentos se puede imaginar de la siguiente manera: la fijación de una variable de argumento corresponde a una restricción del conjunto de definiciones bidimensionales a un subconjunto unidimensional, p. B. , la función resultante corresponde a la intersección de la gráfica de con el plano de todos los puntos . Por lo tanto, también se puede llegar a todos los puntos del gráfico mediante una selección de dos etapas: primero definiendo el plano de corte y luego evaluando la curva de intersección en el punto . ${\ Displaystyle z = f (x, y)}$${\ Displaystyle y = 1}$${\ Displaystyle f (x, y)}$${\ Displaystyle (x, 1, z)}$${\ Displaystyle (x, y, z)}$${\ Displaystyle y = 1}$${\ Displaystyle s (x) = f (x, y) | _ {y = 1}}$${\ Displaystyle x}$

solicitud

Currying se usa principalmente en lenguajes de programación y cálculos, en los que las funciones solo pueden tomar un único argumento. Estos incluyen, por ejemplo, ML , Unlambda y el cálculo lambda, así como el Haskell que lleva el nombre de Curry . Sin embargo, muchos de estos lenguajes ofrecen al programador posibilidades sintácticas para disfrazar esto. Un ejemplo de esto es la equivalencia de la definición de función en el ejemplo que se muestra arriba .

JavaScript

El siguiente ejemplo muestra el currying en JavaScript . Primero, se uncurried_adddefine una función que tiene la suma de los dos argumentos como resultado. Por otro lado, se curried_adddefine una función que devuelve una función definida como cierre que se puede aplicar parcialmente.

function uncurried_add(x, y) {
    return x + y;
}

function curried_add(x) {
    return function(y) {
        return x + y;
    };
}

console.log(uncurried_add(3, 5)); // 8
console.log(curried_add(3)(5)); // 8

const add_three = curried_add(3);
console.log(add_three(5)); // 8
console.log(add_three(12)); // 15

La función se aplica parcialmente a través del currying, mediante el cual los argumentos de la función se pasan uno tras otro y se mantienen temporalmente en una nueva función que se puede usar más.

Las funciones también se pueden definir más brevemente en JavaScript usando la notación lambda:

const uncurried_add = (x, y) => x + y;
const curried_add = x => y => x + y;

Java

import java.util.function.*;

class Main {
    static IntBinaryOperator uncurriedAdd = (x, y) -> x + y;
    static IntFunction<IntUnaryOperator> curriedAdd = x -> y -> x + y;

    public static void main(String[] args) {
        System.out.println(uncurriedAdd.applyAsInt(3, 5)); // 8
        System.out.println(curriedAdd.apply(3).applyAsInt(5)); // 8

        var addThree = curriedAdd.apply(3);
        System.out.println(addThree.applyAsInt(5)); // 8
        System.out.println(addThree.applyAsInt(12)); // 15
    }
}

Kotlin

val uncurried_add = { x: Int, y: Int -> x + y }
val curried_add = { x: Int -> { y: Int -> x + y } }

println(uncurried_add(3, 5)) // 8
println(curried_add(3)(5)) // 8

val add_three = curried_add(3)
println(add_three(5)) // 8
println(add_three(12)) // 15

C ++

C ++ introdujo el cálculo lambda con funciones anónimas al lenguaje. Con la palabra clave auto, el tipo de datos se deriva implícitamente a través de la inferencia de tipos , sin tener que declarar el tipo de datos explícitamente. Esto da como resultado una notación más corta para el plan de estudios:

#include <iostream>

using namespace std;

int uncurried_add(int x, int y) {
    return x + y;
}

auto curried_add(int x) {
    return [x](int y) { return x + y; };
}

int main() {
    cout << uncurried_add(3, 5) << endl; // 8
    cout << curried_add(3)(5) << endl; // 8

    auto add_three = curried_add(3);
    cout << add_three(5) << endl; // 8
    cout << add_three(12) << endl; // 15

    return 0;
}

Tenga en cuenta que la mención del tipo inten el argumento de la expresión lambda también se puede autoreemplazar con, que generaliza la implementación. Sin embargo, los parámetros de la función nombrada curried_addsolo se pueden generalizar utilizando plantillas para diferentes tipos de datos.

C.

Dado que no hay funciones anónimas en el lenguaje de programación C , una función con nombre devuelta por se adddefine por separado curried_add. El valor de xse zalmacena en la variable global porque la función addno puede acceder a la continuación de la función curried_add.

#include <stdio.h>

int uncurried_add(int x, int y) {
    return x + y;
}

int z;

int add(int y) {
    return y + z;
}

typedef int function(int);

function* curried_add(int x) {
    z = x;
    return add;
}

int main() {
    printf("%d\n", uncurried_add(3, 5)); // 8
    printf("%d\n", curried_add(3)(5)); // 8

    function* add_three = curried_add(3);
    printf("%d\n", add_three(5)); // 8
    printf("%d\n", add_three(12)); // 15

    return 0;
}

C #

using System;

class Program {
    delegate int Method(int x, int y);
    delegate Func<int, int> Curry(int x);

    static Method uncurried_add = (x, y) => x + y;
    static Curry curried_add = x => y => x + y;

    public static void Main() {
        Console.WriteLine(uncurried_add(3, 5)); // 8
        Console.WriteLine(curried_add(3)(5)); // 8

        var add_three = curried_add(3);
        Console.WriteLine(add_three(5)); // 8
        Console.WriteLine(add_three(12)); // 15
    }
}

F #

let uncurried_add (x, y) = x + y
let curried_add x y = x + y

printfn "%i" (uncurried_add (3, 5)) // 8
printfn "%i" ((curried_add 3) 5) // 8
printfn "%i" (curried_add 3 5) // 8

let add_three = curried_add 3
printfn "%i" (add_three 5) // 8
printfn "%i" (add_three 12) // 15

Haskell

En el lenguaje de programación Haskell , una función solo puede tener exactamente un parámetro. Si desea llamar a una función con múltiples argumentos, los argumentos primero deben combinarse en un nuevo objeto para que la función reciba solo un argumento. Los parámetros se pueden enumerar entre corchetes separados por comas para definir una tupla .

uncurried_add (x, y) = x + y

Una alternativa a esto es el curry. En la notación explícita, se define una función con un solo argumento para cada valor en la tupla. Siempre que no se hayan pasado todos los argumentos, se devuelve una función que devuelve un resultado parcial.

curried_add x = \y -> x + y

Dado que la notación con varias funciones lambda puede ser engorrosa, existe una notación sintácticamente azucarada que es semánticamente equivalente. Si escribe los argumentos uno detrás del otro sin paréntesis, obtendrá automáticamente una función currificada.

curried_add x y = x + y

La función currificada se puede utilizar tanto explícita como implícitamente en parte.

main = do
    print (uncurried_add (3, 5)) -- 8
    print ((curried_add 3) 5) -- 8
    print (curried_add 3 5) -- 8

    let add_three = curried_add 3
    print (add_three 5) -- 8
    print (add_three 12) -- 15

Además, Haskell ofrece la opción de convertir una función retrospectivamente entre una definición actualizada y una no actualizada. Las funciones curryy uncurryse utilizan para ello.

main = do
    let uncurried = uncurry curried_add
    print (uncurried (3, 5)) -- 8

    let curried = curry uncurried_add
    print ((curried 3) 5) -- 8
    print (curried 3 5) -- 8

    let add_three = curried 3
    print (add_three 5) -- 8
    print (add_three 12) -- 15

pitón

def uncurried_add(x, y):
    return x + y

def curried_add(x):
    return lambda y: x + y

print(uncurried_add(3, 5)) # 8
print(curried_add(3)(5)) # 8

add_three = curried_add(3)
print(add_three(5)) # 8
print(add_three(12)) # 15

Raku

sub uncurried_add($x, $y) { $x + $y }

sub curried_add($x) {
    sub ($y) { $x + $y };
}

say uncurried_add(3, 5); # 8
say curried_add(3)(5); # 8

my &add_three = &curried_add(3);
say &add_three(5); # 8
say &add_three(12); # 15

En el lenguaje de programación Raku existe la posibilidad de currificar un objeto de función solo cuando se llama a la función.

my &uncurried_add = sub ($x, $y) { $x + $y };
say &uncurried_add(3, 5); # 8
say &uncurried_add.assuming(3)(5); # 8

my &add_three = &uncurried_add.assuming(3);
say &add_three(5); # 8
say &add_three(12); # 15

Rubí

def uncurried_add(x, y)
    return x + y
end

def curried_add(x)
    return lambda { |y| x + y }
end

puts uncurried_add(3, 5) # 8
puts curried_add(3).call(5) # 8

add_three = curried_add(3)
puts add_three.call(5) # 8
puts add_three.call(12) # 15

En el lenguaje de programación Ruby, existe la opción de currificar un objeto de función solo cuando se llama a la función.

uncurried_add = lambda { |x, y| x + y }
puts uncurried_add.call(3, 5) # 8
puts uncurried_add.curry[3][5] # 8

add_three = uncurried_add.curry[3]
puts add_three.call(5) # 8
puts add_three.call(12) # 15

Esquema

(define uncurried-add (lambda (x y)
    (+ x y)))

(define curried-add (lambda (x)
    (lambda (y)
        (+ x y))))

(display (uncurried-add 3 5)) (newline) ; 8
(display ((curried-add 3) 5)) (newline) ; 8

(define add-three (curried-add 3))

(display (add-three 5)) (newline) ; 8
(display (add-three 12)) (newline) ; 15

Tcl

En Tcl no es necesario preparar ninguna construcción especial como variantes con curry o sin curry.

En Tcl, una llamada de comando es solo una lista de palabras en las que la palabra de comando está en la primera posición. El operador {*}puede usarse para reemplazar un argumento, que en sí mismo es una lista, con sus elementos en su lugar. Esto significa que una lista que se encuentra en la parte superior de la lista cuando se la llama puede contener cualquier número de argumentos además del comando que se va a llamar.

Currying es, por lo tanto, idéntico a agregar otra palabra a esta lista, y cada {*}llamada que comienza con es una llamada lambda (llamada así por las funciones anónimas a menudo llamadas "expresiones lambda" en otros lenguajes, que se pueden integrar fácilmente de esta manera).

El comando estándar tcl::mathop::+que existe para implementar la sintaxis de la expresión Tcl que no se usa aquí se usa para agregar . Este comando agrega cualquier número de argumentos.

Dado que tiene sentido llevar a cabo tales experimentos en la consola Tcl, aquí no se necesitan declaraciones de impresión explícitas.

tcl::mathop::+ 3 5        ;# 8    direkter Aufruf

set f tcl::mathop::+      ;#      simple "Lambda"-Liste, nur das Kommando
{*}$f 3 5                 ;# 8    Aufruf über "Lambda" in Variable f

lappend f 3               ;#      "Currying" durch Hinzufügen
set f {tcl::mathop::+ 3}  ;#      "Curried" alternativ direkt formuliert
{*}$f 5                   ;# 8    Aufruf über "Curried Lambda"

lappend f 1 2             ;#      mehr Parameter hinzufügen
{*}$f 4 5                 ;# 15 = (3+1+2) + (4+5) ... ganz natürlich

Referencias y comentarios individuales

1. ↑ Moses Schönfinkel : Acerca de los componentes básicos de la lógica matemática. En: Mathematische Annalen 92 (1924). Pp. 305-316, digitalizado .
2. ↑ Gottlob Frege : Leyes básicas de la aritmética. Hermann Pohle, Jena 1893 (Volumen I) 1903 (Volumen II) korpora.org .
3. ↑ Haskell Brooks Curry , Robert Feys, Roger Hindley , Jonathan P. Seldin: Lógica combinatoria. Holanda Septentrional, 2 volúmenes, 1958, 1972.
4. ↑ Esto denota o el conjunto de imágenes desde hasta .${\ Displaystyle (X \ to Y)}$${\ Displaystyle [X \ to Y]}$${\ Displaystyle X}$${\ Displaystyle Y}$
5. ↑ En el caso de cero dígitos (n = 0), el currying asignaría un mapeo sin parámetros y con un valor a un mapeo de un solo dígito con un valor constante , por ejemplo ${\ Displaystyle f}$${\ Displaystyle b \ in B}$${\ Displaystyle b}$

   ${\ Displaystyle f _ {\ mathrm {curry}} \ colon B \ to B, x \ mapsto b}$.

6. ↑ Un ejemplo es con (donde denota la diagonal ).${\ Displaystyle f (a_ {1}, a_ {2}): = a_ {1} / (a_ {1} -a_ {2})}$${\ Displaystyle a_ {1}, a_ {2} \ in \ mathbb {R} \ setminus \ Delta _ {\ mathbb {R}}}$${\ Displaystyle \ Delta _ {\ mathbb {R}}}$ ${\ Displaystyle \ {(a_ {1}, a_ {2}) \ in \ mathbb {R} ^ {2} | a_ {1} = a_ {2} \}}$
7. ↑ En el ejemplo anterior, esto es .${\ Displaystyle \ mathbb {R} \ setminus \ {a_ {1} \}}$
8. ↑ El requisito previo es que el símbolo no esté ya sobrecargado con arity 1 de alguna otra manera (ver ejemplo a continuación, esto hace que sea necesario distinguir entre y ).${\ Displaystyle f}$${\ Displaystyle \ operatorname {mult}}$${\ Displaystyle \ operatorname {prod}}$
9. ↑ Para distinguirlo del marcador de posición , aquí se usa el signo de multiplicación.${\ Displaystyle \ cdot}$${\ Displaystyle *}$
10. ↑ Esta función también podría tener su propio nombre:

    ${\ Displaystyle \ operatorname {doble}: = \ operatorname {mult} _ {\ mathrm {curried}} (2) = \ operatorname {mult} (2, \ cdot) \ colon \ mathbb {N} \ to \ mathbb { NORTE}}$

    con .${\ Displaystyle \ operatorname {doble} (n) = 2 * n}$
11. ↑ Distinguir entre y la función sobrecargada con aridad y factores . Aunque es de dos dígitos , es una función de un solo dígito, mientras que es una función de un solo dígito.${\ Displaystyle \ operatorname {mult}}$${\ Displaystyle \ operatorname {prod}}$${\ Displaystyle \ operatorname {prod} (k_ {1}, \ dotsc, k_ {r}) = \ prod _ {i = 1} ^ {r} k_ {i}}$${\ Displaystyle r}$${\ Displaystyle k_ {i} \ in \ mathbb {N}}$${\ Displaystyle \ operatorname {mult} (m, n) = \ operatorname {prod} (m, n) = m * n}$${\ Displaystyle \ operatorname {prod} (m) = m}$${\ Displaystyle \ operatorname {mult} (m) = \ operatorname {mult} _ {\ mathrm {curried}} (m) = \ operatorname {mult} (m, \ cdot)}$